- Dataset
- Simple Logistic Regression
- Neural Network model
- Loss function
- Back-propogation
- Integrate previous parts nn_model()
In this notebook I build a simple neural network, having a single hidden layer. Next, I compare this model for its classification accuracy to a boilerplate logistic regression.
- Implement a 2-class classification neural network with a single hidden layer
- Use units with a non-linear activation function, such as tanh
- Compute the cross entropy loss
- Implement forward and backward propagation
This notebook was inspired by Andrew Ng's Deep Learning Specialization tutorial on Coursera
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets as datasets
import sklearn.linear_model
import copy as copy
%config InlineBackend.figure_format = 'retina'
%config InlineBackend.print_figure_kwargs={'facecolor' : "w"}
np.random.seed(42) # set a seed so that the results are consistent
Code to make spirals is adapted from:
N = 400 # number of points per class
D = 2 # dimensionality
K = 2 # number of spokes
X = np.zeros((N*K,D)) # data matrix (each row = single example)
Y = np.zeros(N*K, dtype='int') # class labels
for j in range(K):
ix = range(N*j,N*(j+1))
r = np.linspace(0, 1, N) # radius
t = np.linspace(j*4.2, (j+1)*4.2, N) + np.random.randn(N)*0.2 # theta
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
Y[ix] = (0 if j % 2 == 0 else 1)
X = copy.deepcopy(X.T)
Y = copy.deepcopy(Y.reshape(-1,1).T)
fig, ax = plt.subplots(1,1, figsize=(8,8))
# lets visualize the data:
ax.scatter(X[0, :], X[1, :], c=Y.ravel(), s=40, cmap=plt.cm.Spectral)
ax.set_xlabel('$X_1$')
ax.set_ylabel('$X_2$')
ax.set_title('Visualize data')
shape_X = X.shape
shape_Y = Y.shape
print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
clf = sklearn.linear_model.LogisticRegression();
clf.fit(X.T, Y.ravel());
Convenience function to plot a decision boundary for the classification model
def plot_decision_boundary(func, x_input, y_input):
xx_1, xx_2 = np.mgrid[np.min(x_input[:,0]):np.max(x_input[:,0]):.01, np.min(x_input[:,1]):np.max(x_input[:,1]):.01]
grid = np.c_[xx_1.ravel(), xx_2.ravel()]
y_pred_grid = func(grid).reshape(xx_1.shape)
y_pred = func(x_input)
fig, ax = plt.subplots(figsize=(10, 10))
contour = ax.contourf(xx_1, xx_2, y_pred_grid, alpha=0.7, cmap="Spectral")
ax.scatter(x_input[:,0], x_input[:, 1], c=y_pred, s=50, cmap="Spectral", edgecolor="white", linewidth=1)
lims = [np.min([ax.get_xlim(), ax.get_ylim()]), # min of both axes
np.max([ax.get_xlim(), ax.get_ylim()]), # max of both axes
]
ax.set(aspect='equal',
xlim=(np.min(x_input[:,0]), np.max(x_input[:,0])), ylim=(np.min(x_input[:,1]),np.max(x_input[:,1])),
xlabel="$X_1$", ylabel="$X_2$")
plot_decision_boundary(lambda x: clf.predict(x), X.T, Y.T)
plt.title("Logistic Regression")
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y, LR_predictions) + np.dot(1-Y, 1-LR_predictions))/float(Y.size)*100) +
'% ' + "(percentage of correctly labelled datapoints)")
Interpretation: The dataset is not linearly separable, so logistic regression doesn't perform well. Hopefully a neural network will do better.
Neural Network model
Logistic regression did not work well on the dataset. Let's train a Neural Network with a single hidden layer and see if it does any better.
Here is basic framework for the model:
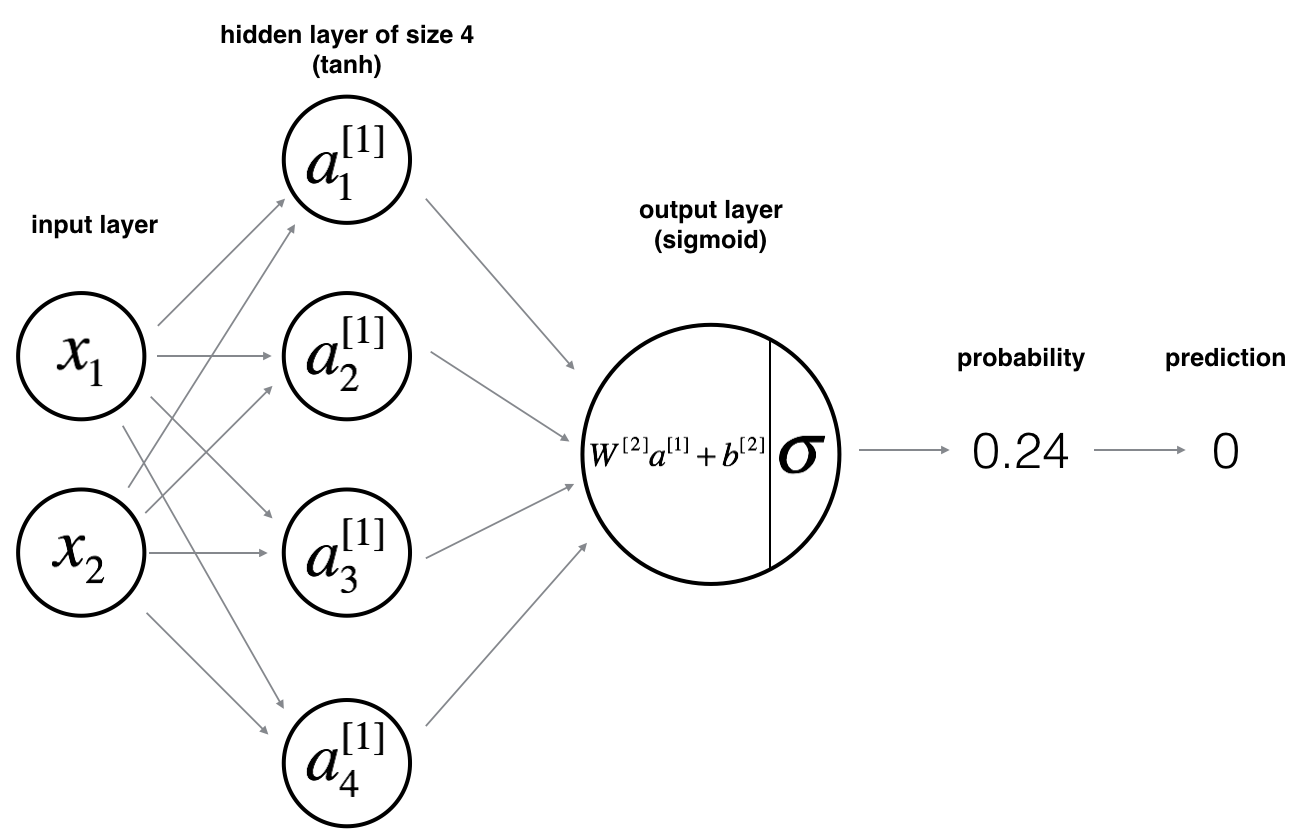
Mathematically:
For one example $x^{(i)}$:
$$ z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1]}\tag{1} $$ $$ a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2} $$$$ z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2]}\tag{3} $$$$ \hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4} $$$$ y^{(i)}_{prediction} = \begin{cases} 1 & \mbox{if } a^{[2](i)} > 0.5 \\ 0 & \mbox{otherwise } \end{cases}\tag{5} $$Given the predictions on all the examples, you can also compute the cost $J$ as follows:
$$ J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6} $$The general methodology to build a Neural Network is to:
- Define the neural network structure ( # of input units, # of hidden units, etc).
- Initialize the model's parameters
- Loop:
- Implement forward propagation
- Compute loss
- Implement backward propagation to get the gradients
- Update parameters (gradient descent)
def layer_sizes(X, Y, n_h=4):
"""
Arguments:
X -- input dataset of shape (input size, number of examples)
Y -- labels of shape (output size, number of examples)
Returns:
n_x -- the size of the input layer
n_h -- the size of the hidden layer
n_y -- the size of the output layer
"""
n_x = X.shape[0] # size of input layer
n_h = n_h
n_y = Y.reshape(-1,1).T.shape[0] # size of output layer
return (n_x, n_h, n_y)
(n_x, n_h, n_y) = layer_sizes(X, Y)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
def initialize_parameters(n_x, n_h, n_y):
"""
Argument:
n_x -- size of the input layer
n_h -- size of the hidden layer
n_y -- size of the output layer
Returns:
params -- python dictionary containing your parameters:
W1 -- weight matrix of shape (n_h, n_x)
b1 -- bias vector of shape (n_h, 1)
W2 -- weight matrix of shape (n_y, n_h)
b2 -- bias vector of shape (n_y, 1)
"""
np.random.seed(42) # we set up a seed so that your output matches ours although the initialization is random.
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h,1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y,1))
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
Forward-pass
Implement forward_propagation():
- Retrieve each parameter from the dictionary "parameters" (which is the output of
initialize_parameters()) by usingparameters[".."]. - Implement Forward Propagation. Compute $Z^{[1]}, A^{[1]}, Z^{[2]}$ and $A^{[2]}$ (the vector of all your predictions on all the examples in the training set).
- Values needed in the backpropagation are stored in "
cache". Thecachewill be given as an input to the backpropagation function.
def sigmoid(x):
z = 1/(1 + np.exp(-x))
return z
def forward_propagation(X, parameters):
"""
Argument:
X -- input data of size (n_x, m)
parameters -- python dictionary containing your parameters (output of initialization function)
Returns:
A2 -- The sigmoid output of the second activation
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
"""
# Retrieve each parameter from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
### END CODE HERE ###
# Implement Forward Propagation
Z1 = np.dot(W1,X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2,A1) + b2
A2 = sigmoid(Z2)
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
Compute the cost function as follows:
$$ J = - \frac{1}{m} \sum\limits_{i = 1}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13} $$def compute_cost(A2, Y):
"""
Computes the cross-entropy cost given in equation (13)
Arguments:
A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
cost -- cross-entropy cost given equation (13)
"""
m = Y.shape[1] # number of example
# Compute the cross-entropy cost
logprobs = np.dot(Y,np.log(A2).T) + np.dot((1-Y),np.log((1-A2)).T)
cost = -logprobs/m
cost = float(np.squeeze(cost)) # makes sure cost is the dimension we expect. E.g., turns [[17]] into 17
assert(isinstance(cost, float))
return cost
Back-propogation
Using the cache computed during forward propagation, now implement backward propagation.
$$ \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } = \frac{1}{m} (a^{[2](i)} - y^{(i)}) $$$$ \frac{\partial \mathcal{J} }{ \partial W_2 } = \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } a^{[1] (i) T} $$$$ \frac{\partial \mathcal{J} }{ \partial b_2 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)}}} $$$$ \frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } = W_2^T \frac{\partial \mathcal{J} }{ \partial z_{2}^{(i)} } * ( 1 - a^{[1] (i) 2}) $$$$ \frac{\partial \mathcal{J} }{ \partial W_1 } = \frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)} } X^T $$$$ \frac{\partial \mathcal{J} _i }{ \partial b_1 } = \sum_i{\frac{\partial \mathcal{J} }{ \partial z_{1}^{(i)}}} $$- $*$ denotes elementwise multiplication.
- Gradients for each later:
- dW1 = $\frac{\partial \mathcal{J} }{ \partial W_1 }$
- db1 = $\frac{\partial \mathcal{J} }{ \partial b_1 }$
- dW2 = $\frac{\partial \mathcal{J} }{ \partial W_2 }$
- db2 = $\frac{\partial \mathcal{J} }{ \partial b_2 }$
def backward_propagation(parameters, cache, X, Y):
"""
Implement the backward propagation using the instructions above.
Arguments:
parameters -- python dictionary containing our parameters
cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
X -- input data of shape (2, number of examples)
Y -- "true" labels vector of shape (1, number of examples)
Returns:
grads -- python dictionary containing your gradients with respect to different parameters
"""
m = X.shape[1]
# First, retrieve W1 and W2 from the dictionary "parameters".
W1 = parameters['W1']
W2 = parameters['W2']
# Retrieve also A1 and A2 from dictionary "cache".
A1 = cache['A1']
A2 = cache['A2']
# Backward propagation: calculate dW1, db1, dW2, db2.
dZ2 = A2 - Y
dW2 = (1/m) * np.dot(dZ2,A1.T)
db2 = (1/m) * np.sum(dZ2,axis=1, keepdims=True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = (1/m) * np.dot(dZ1, X.T)
db1 = (1/m) * np.sum(dZ1, axis=1, keepdims=True)
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
General gradient descent formalism: $$ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$$
where: $\alpha$ is the learning rate and $\theta$ represents a parameter.
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
Updates parameters using the gradient descent update rule given above
Arguments:
parameters -- python dictionary containing your parameters
grads -- python dictionary containing your gradients
Returns:
parameters -- python dictionary containing your updated parameters
"""
# Retrieve each parameter from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
# Retrieve each gradient from the dictionary "grads"
dW1 = grads['dW1']
db1 = grads['db1']
dW2 = grads['dW2']
db2 = grads['db2']
# Update rule for each parameter
W1 = W1 - learning_rate*dW1
b1 = b1 - learning_rate*db1
W2 = W2 - learning_rate*dW2
b2 = b2 - learning_rate*db2
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
Arguments:
X -- dataset of shape (2, number of examples)
Y -- labels of shape (1, number of examples)
n_h -- size of the hidden layer
num_iterations -- Number of iterations in gradient descent loop
print_cost -- if True, print the cost every 1000 iterations
Returns:
parameters -- parameters learnt by the model. They can then be used to predict.
"""
np.random.seed(42)
n_x, n_h, n_y = layer_sizes(X, Y, n_h=n_h)
# Initialize parameters
parameters = initialize_parameters(n_x, n_h, n_y)
# Loop (gradient descent)
for i in range(0, num_iterations):
# Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
A2, cache = forward_propagation(X, parameters)
# Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
cost = compute_cost(A2, Y)
# Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
grads = backward_propagation(parameters, cache, X, Y)
# Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
parameters = update_parameters(parameters, grads, learning_rate = 1.2)
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
def predict(parameters, X):
"""
Using the learned parameters, predicts a class for each example in X
Arguments:
parameters -- python dictionary containing your parameters
X -- input data of size (n_x, m)
Returns
predictions -- vector of predictions of our model (red: 0 / blue: 1)
"""
# Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
A2, cache = forward_propagation(X, parameters)
threshold = 0.5
predictions = (A2 > threshold)
return predictions
It is time to run the model and see how it performs on a planar dataset. Run the following code to test your model with a single hidden layer of $n_h$ hidden units.
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
def plot_decision_boundary_NN(func, x_input, y_input, ax=None):
xx_1, xx_2 = np.mgrid[np.min(x_input[:,0]):np.max(x_input[:,0]):.01, np.min(x_input[:,1]):np.max(x_input[:,1]):.01]
grid = np.c_[xx_1.ravel(), xx_2.ravel()].T
y_pred_grid = func(grid).reshape(xx_1.shape)
y_pred = func(x_input.T)
if ax == None:
fig, ax = plt.subplots(1,1, figsize=(10,10))
contour = ax.contourf(xx_1, xx_2, y_pred_grid, alpha=0.7, cmap="Spectral")
ax.scatter(x_input[:,0], x_input[:, 1], c=y_pred, s=50, cmap="Spectral", edgecolor="white", linewidth=1)
lims = [np.min([ax.get_xlim(), ax.get_ylim()]), # min of both axes
np.max([ax.get_xlim(), ax.get_ylim()]), # max of both axes
]
ax.set(aspect='equal',
xlim=(np.min(x_input[:,0]), np.max(x_input[:,0])), ylim=(np.min(x_input[:,1]),np.max(x_input[:,1])),
xlabel="$X_1$", ylabel="$X_2$")
return ax
plot_decision_boundary_NN(lambda x: predict(parameters, x), X.T, Y.T)
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')
Accuracy is really high compared to Logistic Regression. The model has spirals! Neural networks are able to learn even highly non-linear decision boundaries, unlike logistic regression.
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
ax = plt.subplot(5, 2,i+1)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary_NN(lambda x: predict(parameters, x), X.T, Y.T, ax)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
ax.title.set_text('Hidden Layer of size {} | Accuracy: {}%'.format(n_h, accuracy))